散点图
散点图的简介
散点图也叫 X-Y 图,它将所有的数据以点的形式展现在直角坐标系上,以显示变量之间的相互影响程度,点的位置由变量的数值决定。
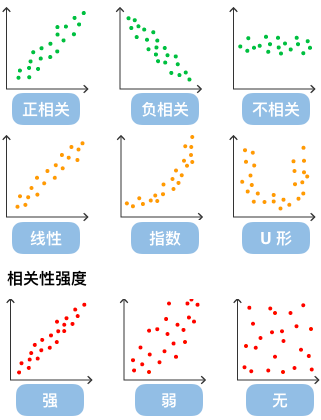
通过观察散点图上数据点的分布情况,我们可以推断出变量间的相关性。如果变量之间不存在相互关系,那么在散点图上就会表现为随机分布的离散的点,如果存在某种相关性,那么大部分的数据点就会相对密集并以某种趋势呈现。数据的相关关系主要分为:正相关(两个变量值同时增长)、负相关(一个变量值增加另一个变量值下降)、不相关、线性相关、指数相关等,表现在散点图上的大致分布如下图所示。那些离点集群较远的点我们称为离群点或者异常点。
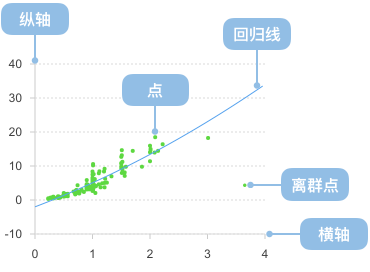
散点图经常与回归线(就是最准确地贯穿所有点的线)结合使用,归纳分析现有数据以进行预测分析。
对于那些变量之间存在密切关系,但是这些关系又不像数学公式和物理公式那样能够精确表达的,散点图是一种很好的图形工具。但是在分析过程中需要注意,这两个变量之间的相关性并不等同于确定的因果关系,也可能需要考虑其他的影响因素。
英文名:Scatter graph, Point graph, X-Y plot, Scatter chart or Scattergram
散点图的构成
| 图表类型 |
散点图 |
| 适合的数据 |
两个连续数据字段 |
| 功能 |
观察数据的分布情况 |
| 数据与图形的映射 |
两个连续字段分别映射到横轴和纵轴。
|
| 适合的数据条数 |
暂无限制 |
| 备注 |
可更具实际情况对点的形状进行分类字段的映射。点的颜色进行分类或连续字段的映射。 |
散点图的应用场景
散点图通常用于显示和比较数值,不光可以显示趋势,还能显示数据集群的形状,以及在数据云团中各数据点的关系。
例子:这里通过男女身高和体重的例子来展示上述所描述的散点图的功能。数据来源丢失,数据不可靠!
| 性别 |
身高(cm) |
体重(kg) |
| 女 |
167.5 |
59 |
| 女 |
161.2 |
51.6 |
| 男 |
176 |
86.4 |
| ... |
... |
... |
| 男 |
180.3 |
82.8 |
(1) 首先对身高和体重两个维度进行比较,可以看到所有的数据点比较集中,呈正相关关系,即身高越高,相应的体重会越大。
$.getJSON('./data/scatter.json',function (data) {
var Stat = G2.Stat;
var frame = new G2.Frame(data);
var hAvg = G2.Frame.mean(frame,'height'); // 计算体重的均值
var wAvg = G2.Frame.mean(frame,'weight'); // 计算身高均值
var lineCfg = { // 线的配置信息
stroke: '#f96a52'
};
var chart1 = new G2.Chart({
id: 'c2',
forceFit: true,
height : 400
});
chart1.source(data);
chart1.col('weight',{
alias: '体重(kg)'
});
chart1.col('height',{
alias: '身高(cm)'
});
chart1.point().position('height*weight').color('#00a3d7').opacity(0.5).shape('circle');
chart1.render();
});
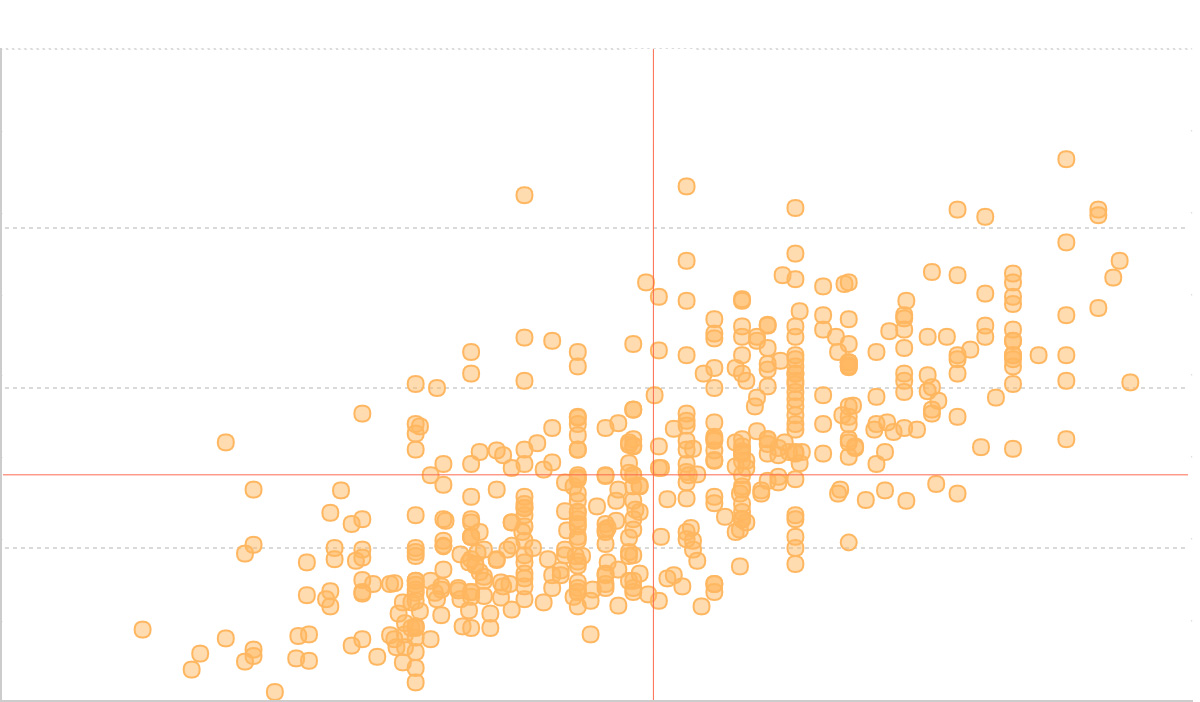
(2) 通过添加平均身高和平均体重的辅助线,将散点图的平面坐标分为四个象限,可以更好得看出数据的分布情况。
$.getJSON('./data/scatter.json',function (data) {
var Stat = G2.Stat;
var frame = new G2.Frame(data);
var hAvg = G2.Frame.mean(frame,'height'); // 计算体重的均值
var wAvg = G2.Frame.mean(frame,'weight'); // 计算身高均值
var lineCfg = { // 线的配置信息
stroke: '#f96a52'
};
var chart2 = new G2.Chart({
id: 'c3',
forceFit: true,
height : 400
});
chart2.source(data);
chart2.col('weight',{
alias: '体重(kg)'
});
chart2.col('height',{
alias: '身高(cm)'
});
chart2.point().position('height*weight').color('#fdb667').opacity(0.5).shape('circle');
chart2.guide().tag([hAvg, 40], [hAvg, 120], '身高平均值: ' + hAvg.toFixed(2), {line:lineCfg});
chart2.guide().tag([140, wAvg], [200, wAvg], '体重平均值' + wAvg.toFixed(2), {line:lineCfg});
chart2.render();
});
(3) 新增一个维度:我们根据性别为每个点加上不同颜色,以展示男女不同性别身高和体重数据的分布。
$.getJSON('./data/scatter.json',function (data) {
var Stat = G2.Stat;
var frame = new G2.Frame(data);
var hAvg = G2.Frame.mean(frame,'height'); // 计算体重的均值
var wAvg = G2.Frame.mean(frame,'weight'); // 计算身高均值
var lineCfg = { // 线的配置信息
stroke: '#f96a52'
};
var chart3 = new G2.Chart({
id: 'c4',
forceFit: true,
height : 400
});
chart3.source(data);
chart3.col('weight',{
alias: '体重(kg)'
});
chart3.col('height',{
alias: '身高(cm)'
});
chart3.point().position('height*weight').color('gender', ['#f96a52', '#00a3d7']).opacity(0.5).shape('circle');
chart3.guide().tag([hAvg, 40], [hAvg, 120], '身高平均值: ' + hAvg.toFixed(2), {line:lineCfg});
chart3.guide().tag([140, wAvg], [200, wAvg], '体重平均值: ' + wAvg.toFixed(2), {line:lineCfg});
chart3.render();
chart3.on('tooltipchange',function(ev){
var items = ev.items;
var origin = items[0];
items.splice(0);
items.push({
name: origin.name,
value: origin.title + ' cm, ' + origin.value + ' kg',
color: origin.color
});
});
});
(4) 同时我们也可以根据样本数据特征计算出回归方程,并为散点图添加回归线。
$.getJSON('./data/scatter.json',function (data) {
var Stat = G2.Stat;
var frame = new G2.Frame(data);
var hAvg = G2.Frame.mean(frame,'height'); // 计算体重的均值
var wAvg = G2.Frame.mean(frame,'weight'); // 计算身高均值
var lineCfg = { // 线的配置信息
stroke: '#f96a52'
};
var chart4 = new G2.Chart({
id: 'c5',
forceFit: true,
height : 400
});
chart4.source(data);
chart4.col('weight',{
alias: '体重(kg)'
});
chart4.col('height',{
alias: '身高(cm)'
});
chart4.point().position('height*weight').color('gender', ['#f96a52', '#00a3d7']).opacity(0.5).shape('circle');
chart4.line().position(Stat.smooth.quadratic('height*weight'));
chart4.render();
chart4.on('tooltipchange',function(ev){
var items = ev.items;
var origin = items[0];
items.splice(0);
items.push({
name: origin.name,
value: origin.title + ' cm, ' + origin.value + ' kg',
color: origin.color
});
});
});
散点图的扩展
我们可以改变数据点形状来表示数据值的区别。
$.getJSON('./data/diamond.json',function (data) {
var chart = new G2.Chart({
id: 'c6',
forceFit: true,
height : 400,
plotCfg: {
margin: [20, 90, 60, 80]
}
});
chart.source(data);
chart.point().position('carat*price').shape('cut').color('cut');
chart.render();
});
$.getJSON('./data/diamond.json',function (data) {
var chart1 = new G2.Chart({
id: 'c7',
forceFit: true,
height : 400,
plotCfg: {
margin: [20, 90, 60, 80]
}
});
var shapes = ['cross','tick','plus','hyphen','line']; // 更换图形类型
chart1.source(data);
chart1.point().position('carat*price').shape('cut',shapes).color('cut');
chart1.render();
});
散点图的扩展
散点图矩阵(scatter plot matrix)是散点图的高维扩展,它从一定程度上克服了在平面上展示高维数据的困难,在展示多维数据的两两关系时有着不可替代的作用。以统计学中经典的鸢尾花案例为例,其数据集包含了50个样本,都属于鸢尾属下的三个亚属,分别是山鸢尾、变色鸢尾和维吉尼亚鸢尾。四个特征被用作样本的定量分析,它们分别是花萼和花瓣的长度和宽度。基于这四个特征的集合,费雪建立了一种线性判别分析法以确定其属种。
| SepalLength(花萼长度) |
SepalWidth(花萼宽度) |
PetalLength(花瓣长度) |
PetalWidth(花瓣宽度) |
Species(属种) |
| 5.1 |
3.5 |
1.4 |
0.2 |
setosa |
| 4.9 |
3.0 |
1.4 |
0.2 |
setosa |
| ... |
... |
... |
... |
... |
| 7.0 |
3.2 |
4.7 |
1.4 |
versicolor |
| 6.4 |
3.2 |
4.5 |
1.5 |
versicolor |
| ... |
... |
... |
... |
... |
| 6.3 |
3.3 |
6.0 |
2.5 |
virginica |
| 5.8 |
2.7 |
5.1 |
1.9 |
virginica |
| ... |
... |
... |
... |
... |
$.getJSON('./data/Iris-flower.json',function(data){
var Stat = G2.Stat;
var chart = new G2.Chart({
id: 'c8',
forceFit: true,
height : 500,
plotCfg: {
margin: [20, 200, 20, 50]
}
});
var items = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth'];
var x = 0;
var y = 0;
for (var v = 0; v < items.length; v++) {
for (var h = 0; h < items.length; h++) {
var view = chart.createView({
index: h + v,
start: {
x: x,
y: y
},
end: {
x: x + 0.2,
y: y + 0.2
}
});
view.source(data);
view.axis(items[h], {
title: null,
labels: null,
line: {
stroke: '#000'
},
tickLine: {
stroke: '#000'
}
});
view.axis(items[v], {
title: null,
labels: null,
line: {
stroke: '#000'
},
tickLine: {
stroke: '#000'
}
});
view.point().position(items[h] + "*" + items[v])
.color('Species', ['#880000', '#008800', '#000088'])
.opacity(0.5)
.shape('circle')
.size(3);
if (v === 3) {
// 横向维度显示
chart.guide().text([x + 0.02, 0.95 - (y + 0.2)], items[h]);
}
x += 0.25;
}
x = 0;
y += 0.25;
// 纵向维度显示
chart.guide().text([x-0.015, 1.07 - y], items[v], {
rotate: -90
});
}
chart.render();
});
散点图与其他图表的对比
这里我们从适用场景和可视化表现两个角度进行对比。
适用场景
- 折线图可以显示随单位(如:单位时间)而变化的连续数据,因此非常适用于显示在相等时间间隔下数据的趋势。
- 散点图显示若干数据系列中各数值之间的关系,或者将两组数绘制为 xy 坐标的一个系列。
可视化表现
- 在折线图中,类别数据沿水平轴均匀分布,所有值数据沿垂直轴均匀分布,即折线图只有一个数据轴(即垂直轴)。
- 散点图有两个数值轴,沿水平轴(x 轴)方向显示一组数值数据,沿垂直轴(y 轴)方向显示另一组数值数据。散点图将这些数值合并到单一数据点并以不均匀间隔或簇显示它们。散点图通常用于显示和比较数值,例如科学数据、统计数据和工程数据。
- 散点图和气泡图都是将两个字段映射到x,y轴的
位置上。散点图侧重于展示点之间的分布规律,而气泡图将数值映射到气泡的大小上,增加了一个维度的数据展示。
- 散点图可以展示成千上万个点的数据,而气泡图为了防止气泡的互相遮挡,需要根据画布的大小控制数据的规模。
散点图的扩展阅读
变型
标签


